Breitensuche-Algorithmus in Java (einfach zu verstehen)
Wer Informatik-Student ist wird genau so wie ich im ersten Semester über den Breitensuche-Algorithmus stolpern (alias Breadth-First-Search bzw. BFS). Im Artikel findet ihr meine wie ich finde sehr gut zu verstehende Implementierung des Algorithmus. Das Projekt findet ihr übrigens auch bei GitHub.
Der Algorithmus ist ein Teil meines Java-Projektes. Wie funktioniert er aber nun? Den Graphen speichere ich intern als eine Menge von Kanten. Jede Kante geht von A nach B, demzufolge sind alle Kanten gerichtet. Ungewichtete Kanten werden über zwei entgegengesetzte gerichtete Kanten realisiert. Erhält mein Algorithmus die Anweisungen von welchem Startknoten aus er welchen Zielknoten suchen soll, so geht er alle Knoten auf einem Level durch und speichert die neu entdeckten Knoten. Sind alle Knoten des aktuellen Levels erforscht so wird das nächste Level geöffnet.
Neue Knoten können nur unter der Bedingung gefunden werden, dass sie nicht bereits besucht wurden sowie nicht in der Menge des aktuellen Knotenlevels sind. Im Bild kann durch letztere Bedingung im 2. Level keine Verbindung zwischen 4 und 3 hergestellt werden. Hintergrund ist, dass die 4 bzw. die 3 ja bereits durch Knoten 1 bekannt sind.
Außerdem wird für jeden Knoten zusätzlich in einer Schlüssel-Wert-Datenstruktur gespeichert durch welchen Knoten er entdeckt wurde. So kann ich am Ende, sofern der Knoten gefunden wurde, den Pfad des kürzesten Weges rekonstruieren. Der kürzeste Weg mit dem BFS-Algorithmus von 0 nach 2 liefert zum Beispiel [2] zurück, weil 2 der Knoten ist, zu dem man sich noch bewegen muss bis zum Ziel. Der Startknoten ist nicht im Pfad enthalten. Aber nun schaut euch erstmal meinen Graphen an:
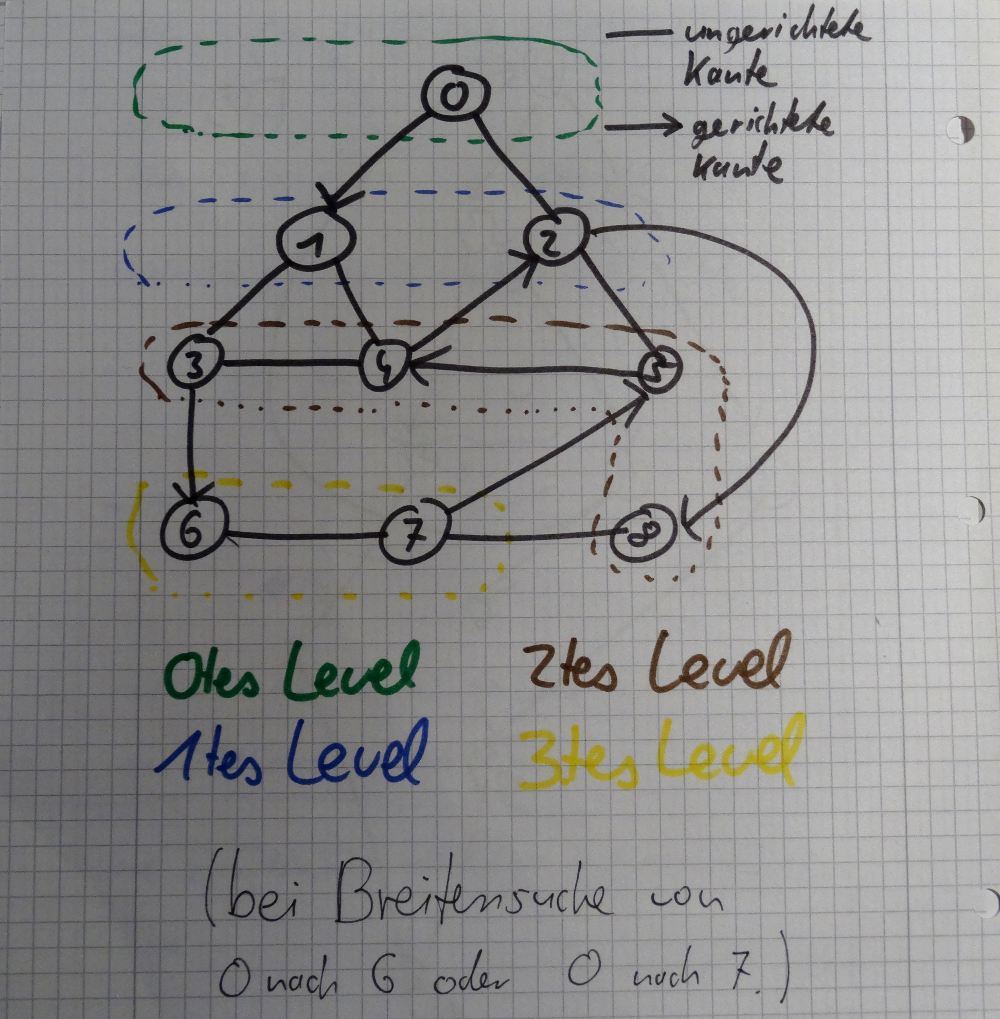
Die Knoten werden nacheinander in mehrere Level aufgeteilt. Pro Level werden alle neuen Knoten gesucht bevor das nächste Level geöffnet wird. Von jedem Knoten werden entsprechend der vorhandenen Kanten Nachbarknoten gesucht.
Wenn ich den Graphen aus dem Bild in Java abbilde, dann schaut das mit meiner Graph-Klasse so aus und liefert folgende Ergebnisse:
public class Main {
public static void main(String[] args) {
Graph g = new Graph();
g.addEdge(0,1); g.addEdge(0,2);
g.addEdge(1,3); g.addEdge(1,4);
g.addEdge(2,0); g.addEdge(2,5); g.addEdge(2,8);
g.addEdge(3,4); g.addEdge(3,6);
g.addEdge(4,3); g.addEdge(4,1); g.addEdge(4,2);
g.addEdge(5,2); g.addEdge(5,4);
g.addEdge(6,7);
g.addEdge(7,6); g.addEdge(7,5); g.addEdge(7,8);
g.addEdge(8,7);
ArrayListStack<Integer> result;
result = g.search(0, 8, SearchAlgorithms.BFS); // [2, 8]
result = g.search(0, 0, SearchAlgorithms.BFS); // []
result = g.search(0, 7, SearchAlgorithms.BFS); // [2, 8, 7]
result = g.search(0, 20, SearchAlgorithms.BFS); // []
result = g.search(8, 0, SearchAlgorithms.BFS); // [7, 5, 2, 0]
}
}Wie bereits erwähnt findet ihr das Projekt auch bei GitHub.
Der Breiten-Suche-Algorithmus in Java
package de.phip1611.graph;
import java.util.HashMap;
import java.util.List;
public class BreadthFirstSearchGraphSearchAlgorithm implements GraphSearchAlgorithm {
@Override
public NodeList search(List edges, Graph.Node startNode, Graph.Node destinationNode) {
NodeList pathNodeList, nodesOnCurrentLevel, nodesOnNextLevel, nodesVisited;
HashMap nodesDiscoveredThrough;
boolean foundNode;
foundNode = false;
pathNodeList = new NodeList();
nodesOnCurrentLevel = new NodeList();
nodesOnNextLevel = new NodeList();
nodesVisited = new NodeList();
nodesDiscoveredThrough = new HashMap<>();
nodesOnNextLevel.add(startNode); // Der STARTKNOTEN
while (!foundNode) {
nodesOnCurrentLevel.clear();
nodesOnCurrentLevel = (NodeList) nodesOnNextLevel.clone();
nodesOnNextLevel.clear();
// gibt nichts mehr zu entdecken
if (nodesOnCurrentLevel.isEmpty()) break;
// die aktuelle Knoten-Generation komplett durchiterieren
for (Graph.Node currentNode : nodesOnCurrentLevel) {
if (foundNode) break;
//System.out.println("Aktiver Knoten: "+currentNode);
//System.out.println("Knoten auf aktiver Ebene:"+ Arrays.toString(nodesOnCurrentLevel.toArray()));
for (Graph.Edge edge : edges) {
//System.out.println("nodes visited: "+nodesVisited);
//System.out.println("nodesVisited.contains(edge.getNodeTo():"+nodesVisited.contains(edge.getNodeTo()));
// alle Kanten die vom aktiven Knoten abgehen herausfiltern
if (edge.getFrom().getKey() == currentNode.getKey()
&& !nodesVisited.contains(edge.getTo())
&& !nodesOnCurrentLevel.contains(edge.getTo())) {
//System.out.println(edge.getNodeTo()+" ist ein durch "+currentNode+" neu entdeckter Knoten");
nodesDiscoveredThrough.put(edge.getTo(),currentNode);
// Folgeknoten durch aktuellen Knoten gefunden
if (edge.getTo() == destinationNode) {
//System.out.println("Knoten gefunden!");
foundNode = true;
break;
} else {
nodesOnNextLevel.add(edge.getTo());
}
}
}
nodesVisited.add(currentNode);
}
}
if (foundNode) {
Graph.Node nodeFoundThroughPrevious = destinationNode;
while (nodeFoundThroughPrevious != startNode) {
pathNodeList.add(0,nodeFoundThroughPrevious);
nodeFoundThroughPrevious = nodesDiscoveredThrough.get(nodeFoundThroughPrevious);
}
}
return pathNodeList;
}
}
0 Comments